Laju Kegagalan Dan Distribusi Laju Kegagalan

By Akbar Prastiko - Juni 04, 2017

Laju Kegagalan Dan Distribusi Laju Kegagalan,

A. Laju Kegagalan (λ)

Laju kegagalan (λ) adalah banyaknya kegagalan per satuan waktu. Laju kegagalan dapat dinyatakan sebagai perbandingan antara banyaknya kegagalan yang terjadi selama selang waktu tertentu dengan total waktu operasi komponen atau sistem. Laju kegagalan terhadap waktu dapat dinyatakan dalam persamaan 1. (Ebeling, 1997)

........................................................ (1)

Laju kegagalan dalam beberapa kasus dapat ditunjukkan sebagai penambahan atau increasing failure rate (IFR), sebagai penurunan atau decreasing failure rate (DFR), dan sebagai konstan atau constant failure rate (CFR), pada saat fungsi laju kegagalan λ(t) adalah fungsi penambahan, penurunan atau konstan. 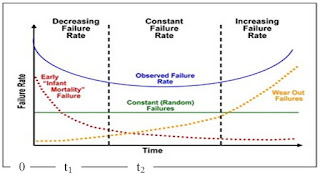Konsep laju kegagalan dilatarbelakangi oleh banyak komponen atau sistem rekayasa yang ternyata menunjukkan perilaku λ(t) mengikuti kurva bak mandi (bathtub curve) seperti gambar 1. Berdasarkan gambar 1, sebuah sistem akan bekerja dengan sejarah hidup yang terbagi dalam tiga masa yaitu: (Dhillon, 2005)

a. Masa Awal (Burn-in)

Pada periode 0 sampai dengan t₁ (permulaan bekerjanya peralatan), kurva menunjukkan bahwa laju kerusakan menurun dengan bertambahnya waktu atau disebut sebagai decreasing failure rate (DFR). Laju kegagalan λ(t) menunjukkan gejala menurun akibat kegagalan dini. Kegagalan tersebut diakibatkan kerusakan dalam manufaktur, retak saat pengelasan, patah, adanya kontaminasi, dan rendahnya kualitas pengendalian. (Ebeling, 1997)

Laju Kegagalan Dan Distribusi Laju Kegagalan

Gambar 1. Kurva Bathtub (Dhillon, 2005)

b. Masa Berguna (Useful Life)

Pada periode t₁ dan t₂ laju kerusakan cenderung tetap atau disebut constant failure rate (CFR). Periode ini biasanya dikenal sebagai useful life period. Komponen menunjukkan λ(t) yang kurang lebih konstan. (Ebeling, 1997)

c. Masa Aus (Wearout)

Pada periode setelah t₂ menunjukkan bahwa laju kerusakan meningkat dengan bertambahnya waktu atau disebut dengan increasing failure rate (IFR). Fungsi laju kegagalan λ(t) menunjukkan peningkatan dimana peluang kegagalan komponen selama interval waktu yang sama menjadi bertambah besar. Kegagalan ini diakibatkan oleh penuaan, korosi, gesekan, sehingga di sebut fase pengausan (wearout). (Ebeling, 1997)

B. Distribusi Laju Kegagalan.

Laju kegagalan dari suatu komponen pada umumnya dinyatakan dalam distribusi statistik, jenis distribusi statistik yang digunakan antra lain adalah sebagai berikut:

1. Distribusi Normal

Distribusi normal yang sering disebut juga dengan distribusi gaussian adalah salah satu jenis distribusi yang paling sering digunakan dalam menjelaskan sebaran data. Probability density function (PDF) dari distribusi normal adalah simetris terhadap nilai rata-rata (mean) dan dispersi terhadap nilai rata-ratanya diukur dengan nilai standar deviasi. Dengan kata lain parameter distribusi normal adalah mean dan standar deviasi. Probability density function dari distribusi normal dapat ditulis seperti persamaan 2. (Ebeling, 1997)

.......................................... (2)

Dengan fungsi keandalan distribusi normal dapat ditulis sebagai berikut:

.......................................... (3)

Dan laju kegagalan dari distribusi normal adalah

....................................... (4)

Gambar 2.9 Pengaruh Standar Deviasi σ (a) Dalam PDF Normal; (b) Dalam Kumulatif Distribusi Normal (Ebeling, 1997)

2. Distribusi Lognormal

Probability density function (PDF) untuk distribusi lognormal dapat ditulis seperti persamaan 5. (Ebeling, 1997)

................................... (5)

Karakteristik distribusi lognormal mempunyai dua parameter yang pertama parameter lokasi (m) dan yang kedua parameter skala (s), sama dengan standar deviasi. Jika distribusi waktu antar kegagalan mengikuti distribusi lognormal, maka: (Ebeling, 1997)

Gambar 2.10 Pengaruh Bentuk Parameter s (a) Dalam PDF Lognormal; (b) Dalam Fungsi Kumulatif Distribusi Lognormal; t_med=1 (Ebeling, 1997)

Fungsi kehandalan distribusi lognormal adalah:

................................... (6)

Laju kegagalan distribusi lognormal adalah:

................................... (7)

Waktu rata-rata kegagalan distribusi lognormal adalah:

................................. (8)

3. Distribusi Weibull

Distribusi weibull telah digunakan secara luas dalam teknik kehandalan. Keuntungan dari distribusi ini adalah bisa digunakan untuk merepresentasikan banyak probability density function (PDF) serta bisa digunakan untuk variasi data yang luas. Karakteristik distribusi weibull:

Mempunyai 2 ( h, b ) atau 3 ( h, b, γ ) parameter, nilai h, b, γ dapat diketahui dari weibull probability paper atau dari software, Saat nilai b= 1 dan γ= 0 weibull akan ekivalen dengan distribusi eksponensial, saat nilai b= 3,44 weibull akan mendekati distribusi normal. Jika distribusi waktu antar kegagalan suatu sistem mengikuti distribusi weibull, maka: (Ebeling,1997)

Fungsi padat peluang probability density function (PFD) distribusi weibull adalah:

................................... (9)

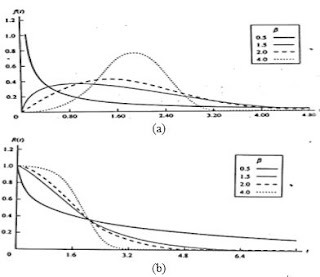
Beta (β) pada distribusi weibull disebut sebagai bentuk parameter. Pengaruh bentuk parameter tersebut

dapat dilihat pada gambar. 4 (a) dengan beberapa nilai berbeda. Probability density function (PDF) untuk β<1, memiliki bentuk yang mirip dengan exponensial, dan untuk nilai β>3 memiliki bentuk seperti distribusi normal. Ketika β=1, λ(t) bernilai konstan dan distribusi ini sama dengan distribusi exponensial dengan λ=1/θ. (Ebeling, 1997)

Gambar 4. Pengaruh dari β (a) Dalam PDF Weibull; (b) Dalam Fungsi Keandalan Weibull. (Ebeling, 1997)

Fungsi kehandalan distribusi weibull adalah:

..................................... (10)

Laju kegagalan distribusi weibull adalah:

.................................... (11)

Saat b<1 akan didapatkan penurunan fungsi laju kegagalan, saat b>1 akan didapatkan peningkatan

fungsi laju kegagalan, b= 1 merupakan fungsi distribusi eksponensial.

Waktu rata–rata kegagalan distribusi weibull adalah:

.................................... (12)

Gambar 5. Pengaruh dari θ (a) Dalam PDF Weibull; (b) Dalam Fungsi Keandalan Weibull (Ebeling, 1997)

4. Distibusi Eksponensial

Fungsi padat peluang probability density function (PFD) distribusi eksponensial adalah: (Ebeling, 1997)

......................................... (13)

Jika distribusi waktu antar kegagalan suatu sistem mengikuti distribusi eksponensial , maka: (Dimitri, 2002)

Fungsi Keandalan distribusi eksponensial adalah

......................................... (14)

Laju kegagalan distribusi eksponensial adalah

....................................... (15)

Waktu rata–rata kegagalan distribusi eksponensial adalah

....................................... (16)

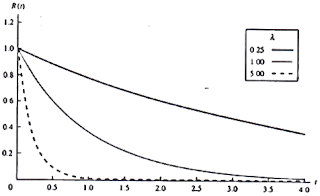
Gambar 6. Fungsi Keandalan Exponensial (Ebeling, 1997)

0 Comments

Laju Kegagalan Dan Distribusi Laju Kegagalan